Zahlenbereich und komplexe Zahlen
Chaos
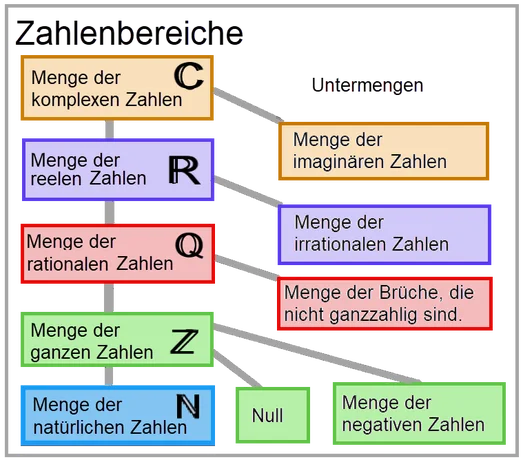
Natürliche Zahlen
Mathematisches Symbol: N
Beispiele: 11, 22, 33, 819567021562
Natürliche Zahlen sind aus dem Grundbedürfnis der Menschen erwachsen, Dinge zu zählen, d. h. die Anzahl von Objekten aus dem Lebensumfeld zu bestimmen.
In den natürlichen Zahlen sind Addition und Multiplikation uneingeschränkt ausführbar.
Ganze Zahlen
Mathematisches Symbol: Z
Beispiele: −7, −1, 0, 1, 7
Die ganzen Zahlen sind eine Erweiterung der natürlichen Zahlen, die es gestattet, uneingeschränkt zu subtrahieren. Dazu werden die natürlichen Zahlen um negative Zahlen ergänzt.
Gebrochene Zahlen
Mathematisches Symbol: Q
Beispiele: 11, 2/7, 9/4
Die gebrochenen Zahlen sind eine Erweiterung der natürlichen Zahlen, die es gestattet, uneingeschränkt zu dividieren. Dazu werden die natürlichen Zahlen um Brüche ergänzt.
Rationale Zahlen
Mathematisches Symbol: Q
Beispiele: 1, −1, 2/7, −2/7, 9/4, −9/4
Die rationalen Zahlen sind einerseits eine Erweiterung der ganzen Zahlen um Brüche als auch der gebrochenen Zahlen um negative Zahlen. In den rationalen Zahlen sind also alle vier Grundrechenarten uneingeschränkt ausführbar.
Reelle Zahlen
Mathematisches Symbol: R
Beispiele: π, e
Die nur eingeschränkte Durchführbarkeit des Wurzelziehens innerhalb der rationalen Zahlen (Irrationalität von √2 = 1,416666…) führte zu der Erkenntnis, dass die rational Zahlen "Lücken" aufweisen. Um diese zu füllen, wurden die reellen Zahlen eingeführt.
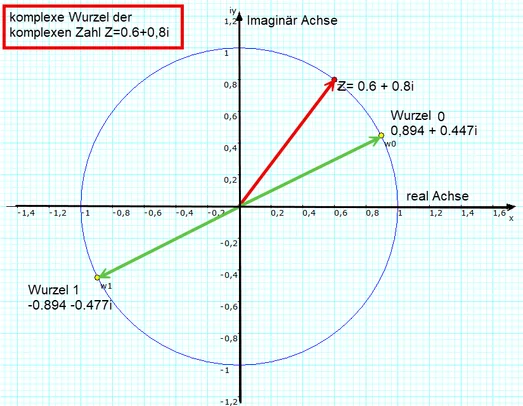
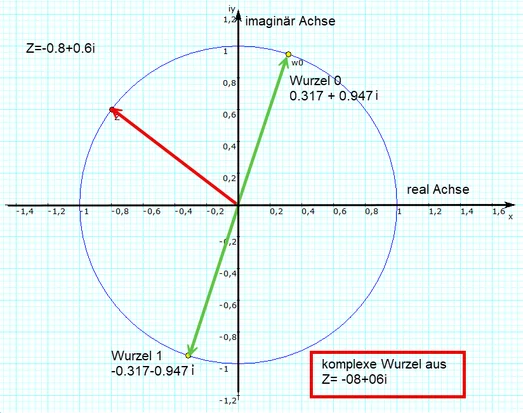
Komplexe Zahlen
Mathematisches Symbol: C
Beispiele: i, 7+3i, 3−4i
Bei der Erweiterung zu den komplexen Zahlen muss man jedoch erstmals auch Eigenschaften aufgeben. Die gewohnte lineare Ordnung der reellen Zahlen, die man sich mittels eines Zahlenstrahls veranschaulichen kann, kann in den komplexen Zahlen nicht mehr aufrechterhalten werden.
Die Erweiterung der reellen Zahlen zu den komplexen Zahlen ist dadurch motiviert, dass z.B. Gleichungen wie x2=−1 nicht lösbar sind. Die Erweiterung wird vorgenommen, indem eine imaginäre Einheit i mit der Definition i2=−1 eingeführt wird.