Populationsgleichung
Chaos

Pierre-François Verhulst (* 28. Oktober 1804 in Brüssel; † 15. Februar 1849) war ein belgischer Mathematiker.
Entdecker der logistischen Gleichung sie wird auch Populationsgleichung genannt.
Pierre-François Verhulst hat sich intensive mir der Population beschäftigt.
Sein 1838 vorgestelltes mathematisches Modell des Bevölkerungswachstums basierte auf Auswertungen vorhandener Statistiken und ergänzte die Theorie des exponentiellen Wachstums durch wachstumshemmende Terme. Er entwickelte es weiter und veröffentlichte es schließlich in einer Arbeit von 1845.
Seit den 1970er Jahren findet Seine Gleichung als ein wichtiges Beispiel der Chaostheorie (er nannte sie die logistische Gleichung).

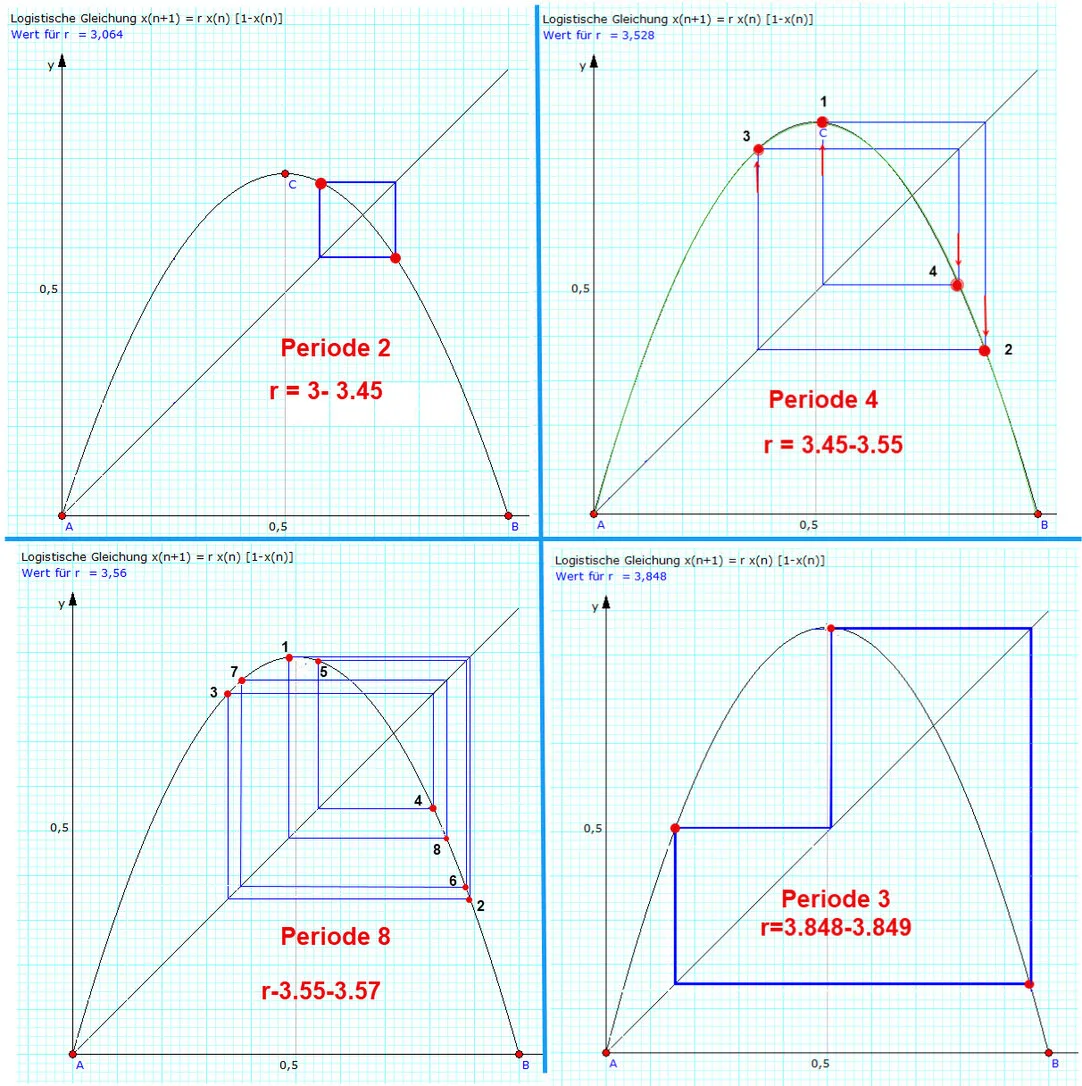
Ansichten der logistischen Gleichung am Beispiel der Peroide 2
Die Feigenbaum Darstellung (x in der vertikalen Achse / r 1-4 auf der Horizintalachse) beginnt links beim Wert 1.5 und steigt stetig an bis r=3. Dann wird die Funktion undifferenzierbar und springt zwischen 2 Werten hin und her dieser Punkt wird Bifurkation genannt. Nach einem fixen Massstab verdoppeln sie diese Teilung die man Periodenverdoppelung nennt.
Die Iterationsdarstellung im gelben Feld (x in der vertikalen Achse / Anzahl Iterationen in der horizontalen Achse). Man erkennt hier das einschwingen (Annäherung an die 2 Endwerte). Die Funktion springt ist nun keine Kurve mehr und somit nicht mehr differenzier bar
Die Darstellung an der Gleichungsfunktion im grünen Feld (auf der vertikalen Achse wird r aufgezeichnet und auf der horizontalen Achse x) Die Punkte zeigen auch die Interationen die sich auf der quadratischen Funktionkurve an die Endwerte springen annähern.