Einführung
Chaos
Definition Mathematischen Chaos
Das Wort Chaos bezeichnet alltags sprachlich zumeist einen Zustand vollständiger Unordnung
oder Verwirrung (Wirrwarr), also fehlender Ordnung bzw. Organisation.
Der folgende Artikel befasst sich mit dem mathematischen Chaos der Systeme. Also ein aus mehreren Einzelteilen zusammengesetztes Ganzes.
Definition des mathematischen Chaos
Beim mathematischen Chaosbegriff
untersucht man das dynamische Verhalten von Systemen,
deren zeitliche Entwicklung unvorhersehbar erscheint,
obwohl die zugrunde liegenden Gleichungen deterministisch sind.
Dieses Verhalten wird als deterministisches Chaos bezeichnet.
Wichtige Fragestellungen im Zusammenhang mit dynamischen Systemen betreffen vor allem ihr Langzeitverhalten
(zum Beispiel Stabilität, Periodizität, Chaos und Ergodizität), die Systemidentifikation und ihre Regelung.
Vereinfachte Erklärung der Chaostheorie
Sie ist ein Teilgebiet der Physik, das den Grenzbereich zwischen Vorhersagbarkeit und „Chaos“ bei sog. nichtlinearen dynamischen Systemen untersucht.
Unter nichtlinearen dynamischen Systemen versteht man solche, die auch Speicherelemente und damit ein „Gedächtnis“ besitzen. Dadurch wird die Systemantwort nicht vom augenblicklichen Wert des Systemreizes allein bestimmt. Sie hängt auch von der Vorgeschichte, also von der Stärke der vorangehenden Erregung ab.
Bei einem linearen System sind Ursache und Wirkung proportional zueinander. Ein Beispiel dafür ist das reibungsfreie Federpendel. Mathematisch gesehen lässt sich das Verhalten eines solchen Systems für alle Zeiten vorausberechnen, sofern nur Position und Geschwindigkeit des Anfangszustands bekannt sind. Ändert man den Anfangszustand ein wenig, ändert sich auch das Systemverhalten nur wenig.
Bei nichtlinearen Systemen ist dies nicht möglich. Für sie gelten zwar ebenfalls eindeutig definierte physikalische Gleichungen. Doch bereits eine winzige Änderung der Anfangsbedingungen kann sich mit der Zeit zu völlig anderen, eben chaotischen Ergebnissen „aufschaukeln“. Außer durch die Unvorhersagbarkeit des Systemverhaltens zeichnen sich chaotische Systeme auch dadurch aus, dass sich bei ihnen spontan selbstähnliche geometrische Strukturen bilden können, die in beliebiger Vergrößerung immer wieder ähnlich aussehen (Fraktale).
Dieses Verhalten wird als deterministisches Chaos bezeichnet.
Dazu später das Beispiel des Doppelpendels.
Als einfaches Beispiel für ein nichtlineares dynamisches Systeme ist die Schaukel (Ps ist aber nicht chaotisch).
Physik des Schaukelns (Hin- und Her-Schwingen ähnlich einem Pendel)
Wird eine Schaukel aus ihrer Ruhelage ausgelenkt, pendelt sie einige Male hin und her, bis die Reibungskräfte ihre Bewegung zum Stillstand bringen.
Energiezufuhr beim Schaukeln durch Heben und Senken des Schwerpunkts
Das Verfahren besteht darin, den Schwerpunkt des eigenen Körpers während der Passagen des tiefsten Punktes nach oben zum Aufhängepunkt hin zu verlagern und in den Momenten des Stillstandes an den Umkehrpunkten wieder zurück. Beim Aufrichten muss Arbeit gegen die Gravitation und die Zentrifugalkraft geleistet werden. Letzteres bewirkt eine Energiezufuhr, die zu einer Erhöhung der Geschwindigkeit am tiefsten Punkt führt und damit die Pendelbewegung antreibt.
Mathematisch formuliert ist dies eine nichtlineare Differentialgleichung 2-ter Ordnung.
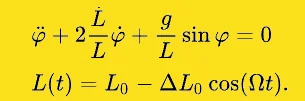 Dabei ist g die Erdbeschleunigung,
Dabei ist g die Erdbeschleunigung, Der nichtlineare Anteil ist die Ursache dafür, dass die Eigenfrequenz von der Schwingungsamplitude abhängt.
Nehmt einfach mit, dass die Pendelbewegung durch Energiezufuhr das Schwingen nichtlinear macht. Damit kann man die Auslenkung steigern.

