Kurven Peano, Koch, Sierpinsky, Cantor
Chaos
Peano Kurve
Die erste flächenfüllende Kurve, wurde von Giuseppe Peano (1858-1932) dem italienischen Mathematiker vorgestellt.Die Welt der Mathematiker war schockiert als Peano seine Kurve 1899 vorgestellt hatte.
Lautes Geschrei!!
Eine Kurve kann niemals eine Fläche sein!!
Sie kann es doch! Das hat sich Giuseppe wie folgt ausgedacht. Die folgenden Bilder zeigen wie dies geht.
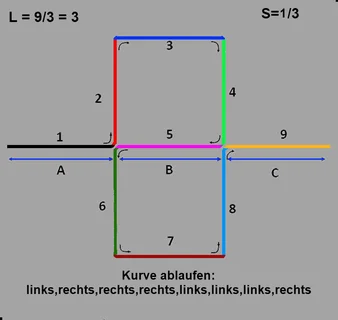L sei die abgelaufene Länge und S der Streckenabschnitt. Die zurückgelegt Stecke A B C ist dann 3S =1/3+1/3+1/3 = 1
Nun iteriert man ... indem man ein Streckenabschnitt mit
der um 1/3 verkleinerten Gesamtkurve ersetzt.
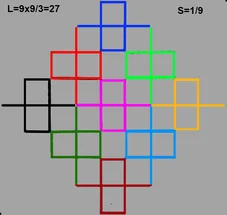
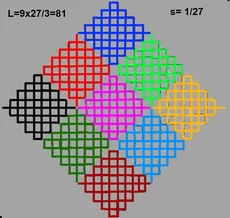
Der Strichdicke ist es zu verdanken, dass bereits nach 3 Iterationen, eine Fläche entsteht.
Sie würde aber auch bei dünner Strichdicke nach x-Iterationen entstehen.
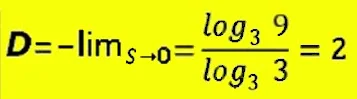Für die Dimension zur Peano-Kurve resultiert 2 > die Kurve ist eine Fläche.Die abgelaufene Länge steigert sich exponentiell und wird theoretisch unendlich lang.
Die ersten Längen sind; 3 >27 >81 > 243 ... also bei jeder Iteration um den Faktor 3 länger.
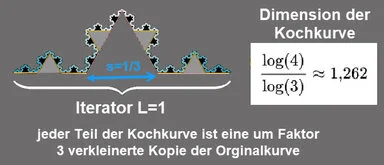
Koch Kurve, Koch Insel
Nils Fabian Helge von Koch (* 25. Januar 1870 in Stockholm; † 11. März 1924 in Danderyd) war ein schwedischer Mathematiker.Er konstruierte die nach ihm benannte Koch-Kurve, eines der ersten Fraktale, als Beispiel für eine unendlich lange, an keiner Stelle differenzierbare Kurve.
Es war das erste formal beschriebene Fraktal.
Dieses Fraktal wurde bei seiner Entdeckung 1904 als Monsterkurve bezeichnet. Die Koch-Kurve ist auch in Form der Kochschen-Insel bekannt,
die durch geeignete Kombination Dreier Koch-Kurven entsteht, sie wird oft auch Schneeflocke genannt.
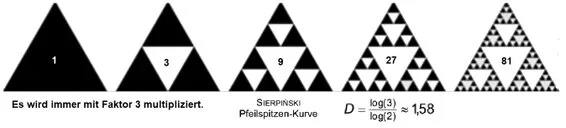
Sierpinski Kurve
Wacław Franciszek Sierpiński (* 14. März 1882 in Warschau; † 21. Oktober 1969 Ebenda) war ein polnischer Mathematiker.Er ist bekannt für seine herausragenden Beiträge zur Mengenlehre (Untersuchungen zum Auswahlaxiom und zur (verallgemeinerten) Kontinuumshypothese), Zahlentheorie, Funktionentheorie und Topologie.
Das Sierpinski-Dreieck ist ein 1915 von Sierpiński beschriebenes Fraktal welches eine selbstähnliche Teilmenge eines meist gleichseitigen Dreiecks ist. Teilt man das Dreieck in vier zueinander kongruente und zum Ausgangsdreieck ähnliche Dreiecke, deren Eckpunkte die Seitenmittelpunkte des Ausgangsdreiecks sind, dann sind die Teilmengen des Fraktals in den drei äußeren Dreiecken skalierte Kopien des gesamten Fraktals, während das mittlere Teildreieck nicht zum Fraktal gehört.
Cantor Staub
Georg Ferdinand Ludwig Philipp Cantor (* 19. Februar in Sankt Petersburg; † 6. Januar 1918 in Halle an der Saale) war ein deutscher Mathematiker. Cantor lieferte wichtige Beiträge zur modernen Mathematik.Insbesondere ist er der Begründer der Mengenlehre und veränderte den Begriff der Unendlichkeit.
Der revolutionäre Gehalt seines Werks wurde erst im 20. Jahrhundert richtig erkannt.
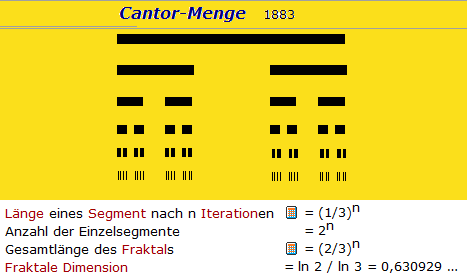
Boxcounting
Wenn eine Kurve nicht selbstähnlich und nicht linear ist z.B. Küstenlinie oder Landesgrenze, dann hilft die Boxcounting-Methode.
Bei der Boxcounting-Methode überdeckt man die Menge mit einem Gitter der Seitenlänge (Raster) s . Wenn N(s) die Zahl der von der Küstenlinie belegten Boxen ist, so ist die Box-Dimension.
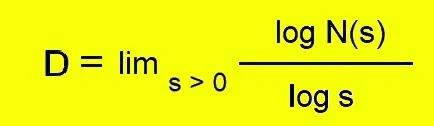
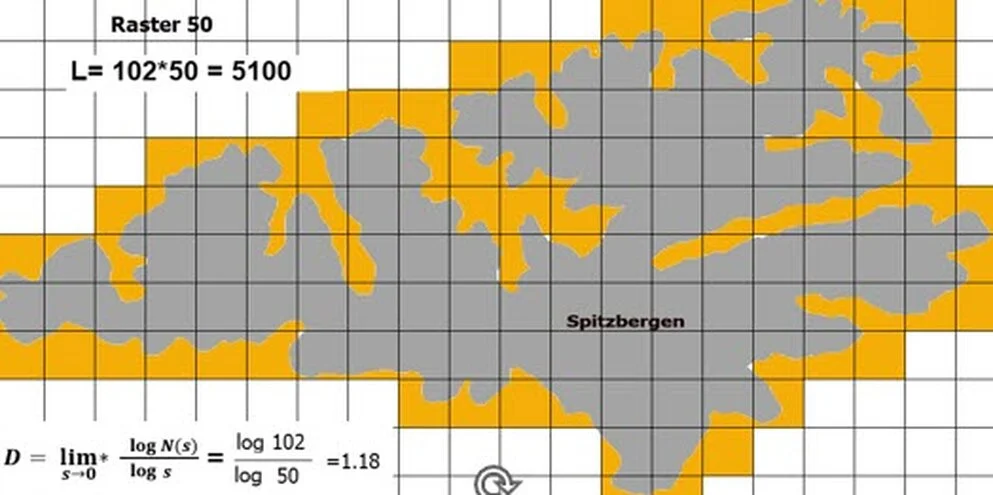
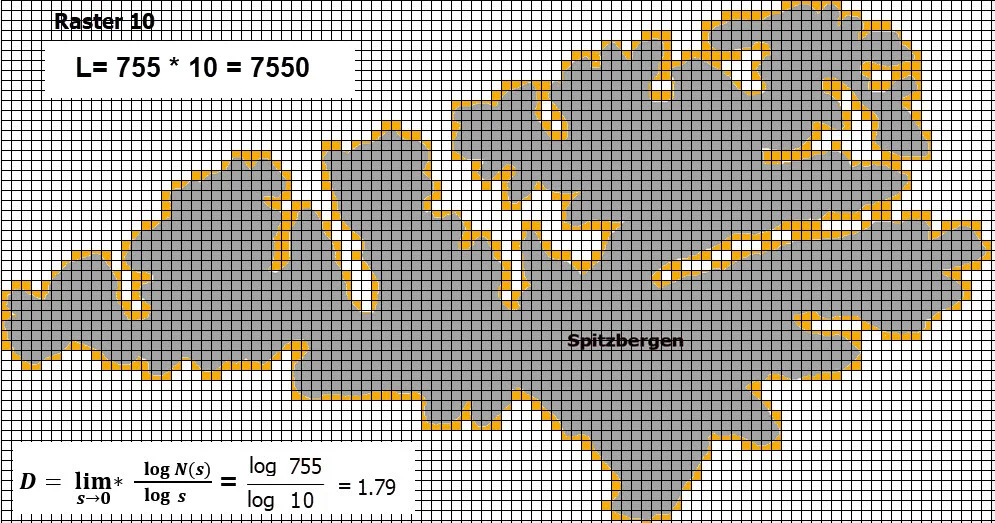
Obwohl die Fläche der Insel endlich ist, ist Ihr Umfang unendlich.
Man löst das Problem, indem man sich auf
den Massstab 1:25000 geeinigt hat.