Bäckertransformation Pointcaré-Transformation
Chaos

Die Grundlage der heutigen Chaosforschung wurde u.a. vom französischen Mathematiker Henri Poincaré (1854-1912) angeregt.
Astronomen verbinden mit dem Namen Henri Poincaré vor allem mit seinen Beiträgen zur Himmelsmechanik.
Poincaré entdeckte auch das deterministische Chaos bei der Analyse der Stabilität des Sonnensystems – einem heute topaktuellen Thema.
Ich möchte aber die verständlichere, aber doch mathematische mysteriöse, Poincaré-Transformation vorstellen.
"Diese Dinge sind so bizarr, dass ich es nicht aushalte, weiter darüber nachzudenken."
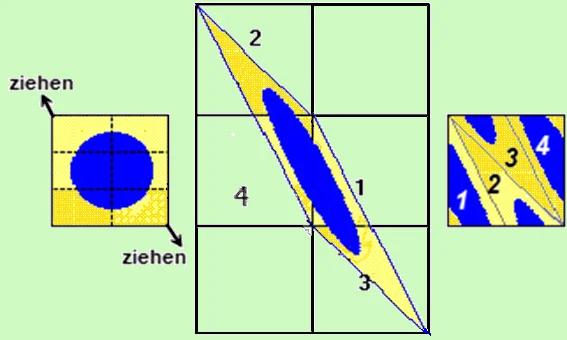
Das Verblüffende ist, dass nach endlich vielen Transformationen (abhängig von der gewählten affinen Abbildung, Matrix) das Originalbild wieder erscheint. Das zwischenzeitlich vorliegende "Chaos" ist damit offensichtlich deterministisch. Mathematisch wird bei jeder derartigen Transformation ein Bildpunkt mit den Koordinaten (x;y) mittels einer Transformationsmatrix verknüpft.
Für die neuen Koordinaten erhält man: x+1 = a * x + b* y und y+1 = c * x + d * y. Die Transformationsmatrix ist beliebig wählbar, wobei zum Erhalt der Flächentreue der Betrag der Determinante gleich +-1 sein muss, d.h. | a * d - b * c | =+- 1.
Heute wird diese Transformation der Bilder auch zum Verschlüsseln von Bildern verwendet.
Matrix Beispiele >> (a=1 / b=1 / c=2 /d= 1) oder (a=1/ b=2/ c=5 /d= 9) oder (a=1000 / b=999 / c=1001 /d= 1000)
Ideal ist ) (a=21/ b=5/ c=38 /d= 9) / Schrittweite 5 / Zyklus-länge 80
Bem: In der Geometrie bezeichnet man als Affinität eine strukturerhaltende Abbildung eines Raumes auf sich selbst.
Das folgende Video zeigt eine solche Transformation mit der Determinanten
a=21/ b=5/c=38 /d= 9

