Systeme die zu Chaos neigen
Chaos
Welche Systeme sind betroffen
Alle nichtlinearen dynamischen Systeme mit mehr als zwei Freiheitsgraden besitzen,
insbesondere viele biologische, meteorologische oder ökonomische Systeme,
können chaotisches Verhalten zeigen und damit über lange Zeiträume unvorhersagbar werden.
Bei nichtlinearen dynamischen Systemen hängt die Systemantwort nicht nur vom augenblicklichen Wert des Systemreizes ab,
sondern auch von der Vorgeschichte, also von der Stärke vorangegangene Erregung.
Ein dynamisches System ist chaotisch, wenn es eine sensitive Abhängigkeit von den Anfangsbedingungen hat.
Beispiele mit wissentlichem chaotischem Verhalten;
Natur:
Turbulenzen / Wetter / Populationsdichte / Erosion / Evolution / Planeten-Beziehungen
Mechanik:
magnetisches Pendel / Doppelpendel / tropfender Wasserhahn
Wirtschaft Verkehr:
Börse / Markt / Verkehrsstau / Nachrichten-Dschungel
Medizin Biologie:
Neurale Netze / Herzrhythmusstörungen / Embolien / Schlaganfall / Tumore
Physik, Chemie:
Laser / Explosion / Chemische Reaktionen
Psychologie:
Stottern / Amokläufe
Ordnung versus Komplexität im Führungsstil
Komplexität und Unvorhersehbarkeit tritt bereits in einfachen Systemen auf, von denen man annehmen könnte eigentlich alles zu wissen.
Der Umgang mit Komplexität erfordert daher einen ganz eigenen Zugang, der das Unvorhersehbare nicht ignoriert, sondern akzeptiert.
Unsere Welt ist komplex!
Dies gilt für alle vernetzte Systeme,
deshalb ist es auch der Umgang mit Ihnen.
Nur Laien und Populisten kennen die einfachen Lösungen,
leider sind sie immer unbrauchbar oder mangelhaft.
soziale Systeme
- Personalführung
- Fanatismus
- Migration
- Unruhen / Kriege
kosmische Systeme
- Turbulenzen
- Wetter
- Populationsdichte
- Erosion
- Evolution
- Planeten-Beziehungen
emergente Systeme
•Zelluläre Automaten
•Lernende Algorithmen
•Digitalisierung
•Künstliche Intelligenz KI
vernetzte Technik
- Soziale Plattformen
- Internet der Dinge
- Big Data
- Big Brother
Eigenschaften komplexer Systeme
Interaktion: Die Wechselwirkungen zwischen den Teilen des Systems sind lokal, ihre Auswirkungen in der Regel global z.B. Kriege, soziale Unruhen, Naturkatastrophen, Lieferketten. Arzneimittelwechselwirkungen …
Emergenz: Bezeichnet die Möglichkeit der Herausbildung von neuen Eigenschaften oder Strukturen eines Systems z.B. Evolution, Ideen, chemische Reaktionen, Internet-Foren, Langtons_Ameise, Curie-Temperatur oder künstliche Intelligenz …
Selbstorganisation: Ist ein Prozess, bei dem aus lokalen Interaktionen zwischen Teilen eines zunächst ungeordneten Systems eine Form der Gesamtordnung entsteht z. B. Kristallisation, thermische Konvektion von Flüssigkeiten, chemische Schwingungen, Tier-schwärme, neuronale Schaltkreise und Schwarzmärkte…
Pfade: Komplexe Systeme zeigen Pfadabhängigkeit: Ihr zeitliches Verhalten ist nicht nur vom aktuellen Zustand, sondern auch von der Vorgeschichte des Systems abhängig z.B. Wetter, Börse, soziale Unruhen…
Selbstregulation: Dadurch können sie die Fähigkeit zur inneren Harmonisierung entwickeln. Sie sind also in der Lage, aufgrund von Informationen und derer Verarbeitung das innere Gleichgewicht und Balance zu verändern
z.B. Heizung, Starkstrom Netze, Leitsysteme…
Offene Systeme: Sie stehen im Kontakt mit ihrer Umgebung und befinden sich fern vom thermodynamischen Gleichgewicht. Das bedeutet, dass sie von einem permanenten Durchfluss von Energie bzw. Materie abhängen
z.B. Kraftwerke, Wetter, Fabrikationsprozesse…
Verhalten eines Systems das man mit Iteration untersucht
Wie
finden man, heraus ob ein dynamisches System chaotisch ist?
Dazu
gibt es leider kein eindeutiger Weg oder eine analytische Formel, sonst hätte
man das Chaos schnell beseitigt.
Vielmehr
hilft es PC-gestützte Simulationsmodelle einzusetzen z.B. mit Iteration.
>>
Iteration (von lat. iterare ,wiederholen)
beschreibt allgemein einen Prozess mehrfachen Wiederholens gleicher oder
ähnlicher Handlungen zur Annäherung an eine Lösung oder ein bestimmtes Ziel.
>>
Iterator: Man startet das System
mit der Anfangsbedingung Xn.
Wendet darauf die Funktionsgleichung des Systems an. Erhält somit ein Resultat
das man als neue Anfangsbedingung Xn
+1 einsetzt.
Ein nichtlineares dynamisches System hat folgenden Verhaltensweisen.
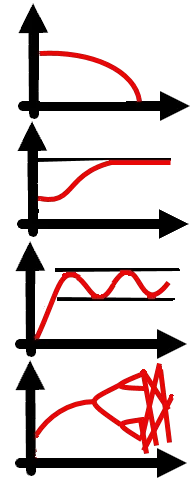
Strebt gegen Null d.h. Stirbt ab oder kommt zum Stillstand.
Stabilisiert sich auf einen Sollwert (Systemstabilität).
Pendelt sich zwischen zwei Zuständen in einem Band ein (Bifurkation oder Schwingung).
Wird ab einem bestimmten Zustand chaotisch.