Fraktale & Selbstähnlichkeit
Chaos
Fraktale Dimension& Selbstähnlichkeit
Zwei Begriffe sind wesentlich, um die fraktale Welt zu verstehen.
Es sind dies die Dimension und die Selbstähnlichkeit.
Dimension
Die Dimension ist ein Konzept in der Mathematik, das die Anzahl der Freiheitsgrade in einem
bestimmten Raum bezeichnet.
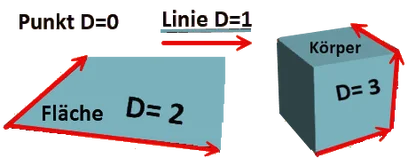
Das ist die Dimension nach Euklid wie wir sie von der Schule her kennen. Die gilt nach wie vor.
Nun gibt es aber Kurven oder Flächen, die sich mit den bestehenden Freiheitsgraden nicht mehr beschreiben lassen.
Dimension ist ein sehr breit diskutiertes Thema; Mathematiker wie Hammel, Hilbert, Lebesgeue, Krull und Hausdorff alle haben Definitionen aufgestellt, die Ihre Berechtigung für spezielle Betrachtungen haben.
Für die Fraktale Dimension ist Hausdorff und die praktisch identische Änlichkeitsdimension zutreffend.
Der Mathematiker Felix Hausdorff (1868 bis1942) aus Breslau legte den Grundstein für das Verständnis der gebrochenen Dimensionen.Wenn ein beliebiges Gebilde durch eine Anzahl Kugel im Raum oder Kreise in der Fläche überdeckt werden kann,
dann ist die Anzahl N(s) proportional zum Radius 1/sD und nach der Dimension D aufgelöst ergibt
die Hausdorff Dimension (die gebrochene Dimension).
Um ein genaues Ergebnis zu erhalten, muss man den Radius möglichst klein halten.
Die Mathematiker sagen dazu Limes (der Grenzwert) strebt gegen Null.
Dazu hat Benoît Mandelbrot (1924 / 2010) den Begriff "Fraktal" definiert und die fraktale Geometrie verfasst.
Was ist der Unterschied von Normalen Gebilden zu fraktalen Gebilde?
"Normale" Gebilde haben die Eigenschaft, dass man ab einer bestimmten Auflösung alle Details erkennen kann.
Fraktale unterscheiden sich genau in dieser Hinsicht, denn bei Fraktalen kann man beliebig kleine Teilbereiche (engl.: " fractions ") betrachten und bekommt immer wieder gleichermaßen komplizierte Strukturen zu Gesicht. Normalerweise sieht das, was man in verschiedenen Auflösungen sieht, immer wieder ähnlich aus. Diese Selbstähnlichkeit ist ebenfalls eine typische Eigenschaft von Fraktalen.
Selbstähnlichkeit
Der Begriff Selbstähnlichkeit ist relativ Neu und erst seit 2010 so populär worden.
Definition:
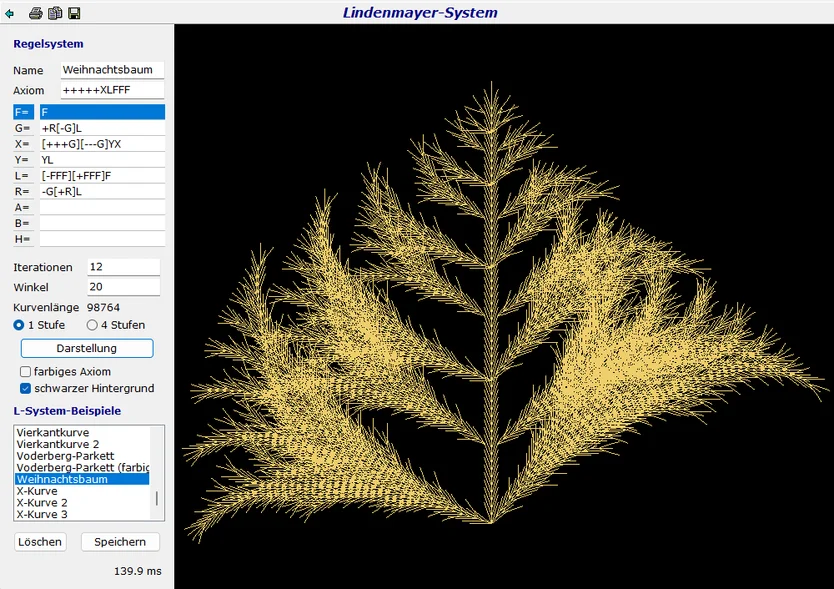
Mengen, die aus N um den Faktor r<1verkleinerte Versionen ihrer selbst bestehenheißen selbstähnlich.Vereinfacht gesagt; Ihr Ganzes besteht aus verkleinerten Teilen des Ganzen.Diese Bilder zeigen was gemeint ist.Die Natur ist voller selbstähnlicher Pflanzen. Am besten erkennbar ist es an schnell wachsenden Pflanzen, da diese von einem homogeneren Klima beeinflusst sind, als langsame über Jahre hinweg wachsende Pflanzen wie z.B. Bäume.Der ungarische Biologe Aristid Lindenmayer hat sich eingehen mit den "Bauplänen der Natur" befasst.Aristid Lindenmayer (* 17. November 1925 in Budapest; † 30. Oktober 1989) war ein ungarischer theoretischer Biologe.
1968 entwickelte er eine formale Sprache als Grundlage einer axiomatischen Theorie biologischer Entwicklung.In jüngerer Zeit fanden die Lindenmayer-System oder L-System genannten Systeme Anwendung in der Computergrafik bei der Erzeugung von Fraktalen und in der realitätsnahen Modellierung von Pflanzen.Das wesentliche Prinzip von L-Systemen besteht in der sukzessiven Ersetzung von Einzelteilen eines einfachen Objektes mittels sogenannter Produktionsregeln. Diese Ersetzungen können rekursiv durchgeführt werden. Damit gehören L-Systeme zu den sogenannten Ersetzungssystemen.
Das ist ein Farn generiert mittels L-System Computerprogramm.Selbstähnlichkeit in der MathematikDie definiert sich durch;
kopieren,skalieren& affin zusammensetzen
Affinität ist eine strukturerhaltende Abbildung auf sich selbst.Beispiel;
Definition:
Der Iterationsprozess besteht in der wiederholten Anwendung derselben Funktionmit einer Rückkopplung des Resultates.Xn ist der Anfangswert und Xn+1 das Resultat der 1. Iteration.
In der numerischen Mathematik benutzt man die Iterationsmethode umsich der exakten Lösung eines Problems schrittweise anzunähern(sukzessive Approximation genannt).Mit dem heutigen Computer, kann man in mathematischen Simulations-Modellenfast bis zur Unendlichkeit iterieren.Was uns ermöglicht komplexe Vorgänge besser zu verstehen.
